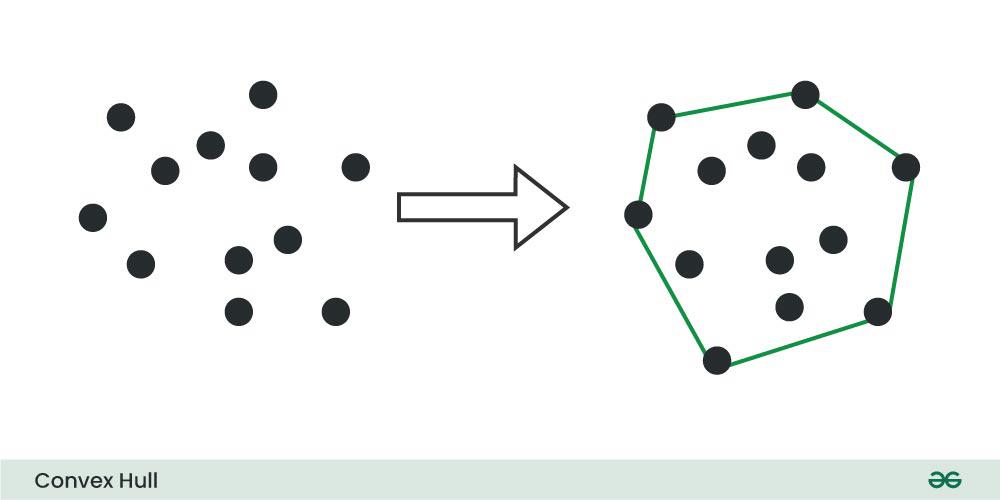
This one took some time. I needed to find the convex hull of a set of points. A convex hull is the set of points that if you were to stretch a rubber band around all the points, its the set of points that the rubber band touches. In this case we are trying to find the perimeter of those points. 

Okay so I did some research and found that Graham Scan can do this and found this set of steps.

1. Choose a Starting Point

    Pick the point with the lowest y-coordinate (and lowest x if tied). This serves as the anchor or pivot.

2. Sort the Other Points

    Sort all other points based on the angle they make with the pivot point (usually using the arctangent or cross product for orientation).

3. Scan and Build the Hull

    Initialize a stack with the first two sorted points.

    Iterate over the rest:

        For each point, check the turn direction with the last two points on the stack (using cross product).

        If it makes a right turn (non-counter-clockwise), pop the last point off the stack.

        Push the current point on the stack.

4. Result

    After processing all points, the stack contains the convex hull — the outer ring in counter-clockwise order.

I knew that I wouldn't just be able to figure this out on my own so I really wanted to see if I could program the solution knowing the steps.

1. Choose the starting point.
     def find_lowest(list) do
        pivot = Enum.reduce(list, hd(list), fn [x, y], [x_acc, y_acc] -> 
          cond do
            y < y_acc -> [x, y] # If the y is lower replace the acc
            y == y_acc and x < x_acc -> [x, y] # If the y is equal pick the lowest x
            true -> [x_acc, y_acc] # If neither is true pass on the acc
          end
        end)
      
        list = Enum.reject(list, &(&1 == pivot))
        {pivot, list}
    end

Okay so we needed to find the lowest point to start from. In this case we wanted to find the lowest y and if there is a tie the lowest y then x.

This is a simple algorithm that will sort through all the points and find the lowest. 

2. Sort based off the cross product
    def cross_product([x0, y0], [x1, y1], [x2, y2]) do
        (x1 - x0) * (y2 - y0) - (y1 - y0) * (x2 - x0) # This is the expression for the cross-product for 3 points
    end
    
    def sort_by_cross({pivot, points}) do
        sorted = Enum.sort(points, fn a, b -> 
            cross_product(pivot, a, b) > 0
        end)
        [pivot | sorted]
    end

This one needed the cross product as a helper function and then used the Enum.sort(), Sort will naturally go through each set of points and use the value for the fn that we have set up.

3. Iterate of the list starting with the first 2 point and popping any point that doesn't fit the right evaluation.
    def hull_loop(points) do
        Enum.reduce(points, [], fn point, acc ->
          acc = pop_until_left_turn(acc, point) # See function below for the algorithm
          [point | acc]
        end)
        |> Enum.reverse() 
      end
      
    defp pop_until_left_turn([b, a | rest], point) do # We want the cross product to to be > 0
        if cross_product(a, b, point) <= 0 do # We want to continue to try points till we get > 0
          pop_until_left_turn([a | rest], point) # This will recursively go through the sorted list till we find the right one.
        else
          [b, a | rest]
        end
      end
      
    defp pop_until_left_turn(acc, _point), do: acc # This is our base case for the recursion

This uses 2 helper functions as well as the reduce that will return the points that are on the outside of the Convex Hull

4. Find the perimeter of the Convex Hull.

    defp distance([[x1, y1], [x2, y2]]), do: :math.sqrt(:math.pow(x2 - x1, 2) + :math.pow(y2 - y1, 2))
    
    def total_length(list) do
        list = list ++ [hd(list)] # I made sure the list has the first point at the head and the end.
        Enum.chunk_every(list, 2, 1, :discard)
        |> Enum.map(fn points -> 
            distance(points) # Run through the distance for all the pairs.
        end)
        |> Enum.sum() # Sum the list of distances.
    end

This is pretty simple once you have the right formula for the distance between 2 points.

 This one was pretty fun to go through as each step was functions that I was able to follow my nose and get to the right solution. Keep in mind that there was many times that I had to insert IO.inspects() to keep track of the data and the format that I was getting from functions.