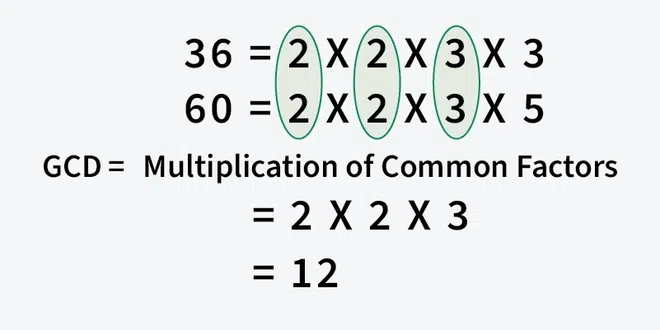For this one we are given 2 sets of integers that multiply to the numbers that we want to find the GCD of. 
input:
5
2 2 3 3 25
4
8 1 6 170
output:
60

So I did this one in a few steps. I wont go over the way I parsed the input, and Ill assume that you have a list of the integers you are finding the factors of.
    defp set_divisors(integers) do # This is a list of integers
        Enum.map(integers, &find_divisor(&1)) # For each integer find the divisors
    end
    
    defp find_divisor(1), do: [] # 1 doesn't have a Prime factorization
    defp find_divisor(n), do: prime_factors(n, 2) # If not 1 start the loop
    
    defp prime_factors(1, _), do: [] # Base-case If you end up with 1 as a test
    defp prime_factors(n, factor) when rem(n, factor) == 0 do 
    # If the factor is divisible find how many it take to get to the number
      [factor | prime_factors(div(n, factor), factor)] # This will add in the an other factor to the list
    end
    
    defp prime_factors(n, factor), do: prime_factors(n, factor + 1)
    # This is for if we find a factor that doesn't work try the next number or if the number has pulled all
    # the factor out of the number. Then we move on to the next number till we have all the factors out. 

Look to the # Comments, to see more info that what I post here. The logic here is that we are testing (starting at 3 and going up from there) to see if the number to test is divisible by the factor. 

If it is you will then keep recursively test more and more of that factor. Once you get to 1 you are done and have pulled all of that factor.

There is two cases where you would find yourself in the last function clause:
You have taking all the factor out of the number;
find_divisor(12)
# → prime_factors(12, 2)
# → rem(12, 2) == 0 → [2 | prime_factors(6, 2)]
# → rem(6, 2) == 0 → [2 | prime_factors(3, 2)]
# → rem(3, 2) != 0 → try factor 3 --- See here
# → rem(3, 3) == 0 → [3 | prime_factors(1, 3)]
# → prime_factors(1, 3) → []

# Final result: [2, 2, 3]

or the initial test doesnt work it will increase the factor by 1 and continue;
find_divisor(15)
# → prime_factors(15, 2)
# → rem(15, 2) != 0 → try next factor: 3
# → rem(15, 3) == 0 → [3 | prime_factors(5, 3)]
# → rem(5, 3) != 0 → try next factor: 4
# → rem(5, 4) != 0 → try next factor: 5
# → rem(5, 5) == 0 → [5 | prime_factors(1, 5)]
# → prime_factors(1, 5) → []

# Final result: [3, 5]

Okay so now we have the factors (prime) for each number. Now we need to map the divisors.
    defp map_divisor_list(divisors) do
        divisors
        |> List.flatten()
        |> Enum.reduce(%{}, fn divisor, map -> 
            Map.update(map, divisor, 1, &(&1 + 1))
       end) 
    end
We start with a list of lists that are the factors of each number. We don't need the lists in a list so we can flatten to start. Once we have that I wanted to get the count of the each number. 

Now that we have the 2 maps, we need to find the common factors and find the amount they have in common.
    def find_common([number_map1, number_map2]) do
        Enum.reduce(number_map1, [], fn {key, value}, acc ->
            case Map.get(number_map2, key) do
              nil -> acc
              v2 -> [pow(key, min(value, v2)) | acc]
            end
        end)
        |> multiply()
        |> rem(@mod)
    end

    defp multiply(common_factors) do
        Enum.reduce(common_factors, 1, &(&1 * &2))
    end

Okay so this is the function for testing the commonality of the factors. Remember that you now have 2 maps that have the count of each factor. So we need to test each number to see if its in the other map. If it is; find the min of the 2 counts and take that factor to its count (#^count). If it isn't ignore it. What is nice about this approach (why you don't have to check the other way) is that we only care about factors that are in both lists.

This takes us to the |> Multiply
This basically just takes all the values in the list and multiplies them together.

Output is up to the reader.