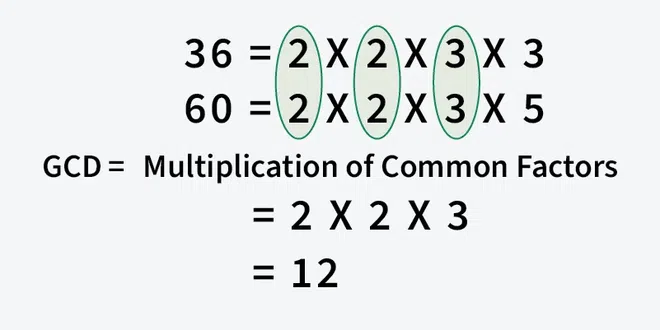For this one we are given 2 numbers and we need to be able to find the number of common divisors. So I went and did a little digging and found that All common divisors of two numbers a and b are exactly the divisors of their GCD.

So we need to find the GCD and then test the common divisors.

Sample Input
3
10 4
1 100
288 240
Sample Output
2
1
10

So lets start with the GCD part:
  def count_common_divisors(pairs) do
    Enum.map(pairs, fn [a, b] ->
      a
      |> Integer.gcd(b)
      |> count_divisors()
    end)
  end

Pretty simple as Elixir has a standard lib for that.

Now for the divisors part:
  def count_divisors(1), do: 1 # case for 1 as its a very small lists

  def count_divisors(n) do 
    1..trunc(:math.sqrt(n)) # you only need to test to the sqrt
    |> Enum.reduce(0, fn i, acc ->
      cond do
        rem(n, i) != 0 -> acc # skip if it doesn't divide
        i * i == n -> acc + 1 # if its a root only add once
        true -> acc + 2 # If its not a root add twice as we will be missing the other number
      end
    end)
  end
 

One thing that I will add here is the reason you only need to go to the sqrt. Think about it this way, if you check for a number like 2 on the number 16, 

16 / 2 == 8
16 / 3 !! doesnt work
16 / 4 == 4

We now have all the pairs for this. If it isn't a square root you need to add 2 as you will be missing it's pair.
If it is a square root then all you need to do is add 1 as the other pair is the same number.