So this is one of the harder ones I've done so far. This required that we not only build a tree structure but also be able to swap nodes on the tree at a specific depth.

A binary tree is a tree which is characterized by any one of the following properties:

    It can be an empty (null).
    It contains a root node and two subtrees, left subtree and right subtree. These subtrees are also binary tree.

Inorder traversal is performed as

    Traverse the left subtree.
    Visit root (print it).
    Traverse the right subtree.

We define depth of a node as follow:

    Root node is at depth 1.
    If the depth of parent node is d, then the depth of current node wll be d+1.

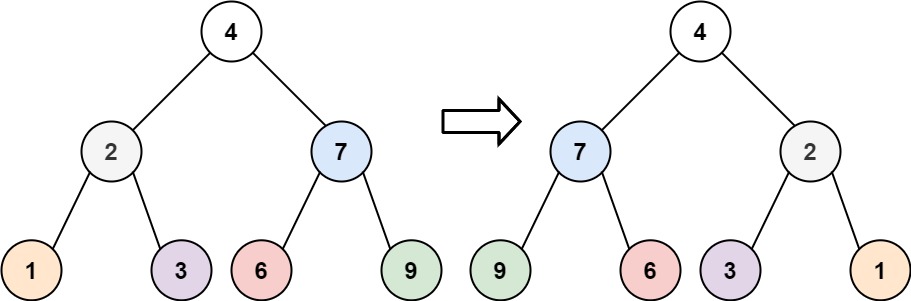
Swapping: Swapping subtrees of a node means that if initially node has left subtree L and right subtree R, then after swapping left subtree will be R and right subtree L.

Eg. In the following tree, we swap children of node 1.

Input
3
2 3
-1 -1
-1 -1
2
1
1

Output
3 1 2
2 1 3

Okay so let's get started. First we need to build the tree map. I wanted it to be a nested map such that we have:
value
depth,
left (child)
right (child)

were the child is an other map that follows the same format.

This required a bit of recursion and using incidences to get the the right child.
    def build_tree(%{nodes: nodes}) do # Starter function to set the first depth
        build_subtree(1, nodes, 1)
    end
      
    # This is the base case for when we reach the end of a branch
    def build_subtree(-1, _nodes, _depth), do: nil
    
    # This is the recursion see the explanation below
    def build_subtree(value, nodes, depth) do
        {left, right} = Enum.at(nodes, value - 1)
        %{
            value: value,
            depth: depth,
            left: build_subtree(left, nodes, depth + 1),
            right: build_subtree(right, nodes, depth + 1)
        }
    end

So for this we need to build each side recursively, we know the depth of the child because we wont go any further within a child if the value is -1. This also works because of how the input is structured as you go down the left to the end then the right. 

{left, right} = Enum.at(nodes, value - 1) 
# This line works as we use the value of the node as the index and because no value should repeat

Okay so now we have our tree and we need to perform the swaps.
    def swap_loop(nil, _k), do: nil

    def swap_loop(%{value: value, depth: depth, left: left, right: right}, k) when rem(depth, k) == 0 do
    %{
        value: value,
        depth: depth,
        left: swap_loop(right, k), 
        right: swap_loop(left, k)
    }
    end

    def swap_loop(%{value: value, depth: depth, left: left, right: right}, k) do
    %{
        value: value,
        depth: depth,
        left: swap_loop(left, k),
        right: swap_loop(right, k)
    }
    end

Remembering the format of each node, we can see that we are going from the top to each node further down. We are then checking at each step for the depth to match the required value that is given, if so then swap the left and right and continue on. If the child is nil be sure to return nil so that we no longer go further down the children. 

Okay so now we need to print the tree. In most cases the puts will only output a single integer then a "\n" so I wanted to be able to join the values then print.
    def print_tree(nil), do: []
    def print_tree(%{value: value, depth: depth, left: left, right: right}) do
        print_tree(left) ++ [value] ++ print_tree(right)
    end

This will go through each side then put it all together. Again going down the left side then the right.

Lastly as it wants use to print the new tree after every swap Ill show the code for keeping the tree up to date after each swap. This goes with the swap_loop function as the starter.
    def swap_starter(tree, swaps) do
        Enum.reduce(swaps, tree, fn swap, acc_tree -> 
            new_tree = swap_loop(acc_tree, swap)
            new_tree
            |> print_tree
            |> puts
            new_tree
        end)
    end

As you can see the accumulator is the tree itself. We perform the swaps then print and then go on to the next swap in the list.